Ivanomata are cellular automata with increasing resolution. Apparently, these didn't exist before, so I named them after myself. If you've seen something similar, let me know and I'll rename them.
One night I was reading the book "The Algorithmic Beauty of Plants" and realized that cellular automata are a special case of context-sensitive L-systems! And for two years I'd tried and couldn't figure out how to make generative grammars two-dimensional.
I was so inspired that the next morning I wrote a prototype.
How it works
A cellular automaton needs rules by which cells change colors.
We only have two colors: ■ and □. To find a new cell color, we look at the color of the cell itself and its four neighbors. There are 32 possible combinations:
Each of these combinations is matched with a color to repaint the central cell — these are our rules. For example, like these:
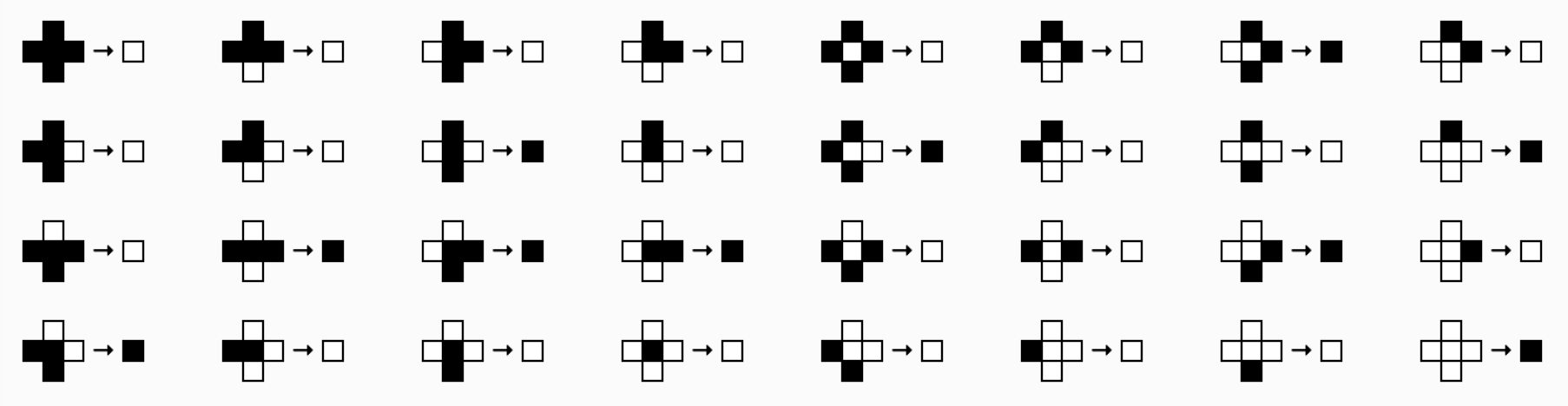This is one of 232 = 4,294,967,296 possible rule variants
The rest is simple. Take a 4×4 cell grid, randomly fill it with □ and ■.
Apply the rules, find new colors for each cell. Notice how the central cell of the shaded area used the matching rule to find its new color.
Finally, increase the grid resolution: divide each cell into four.
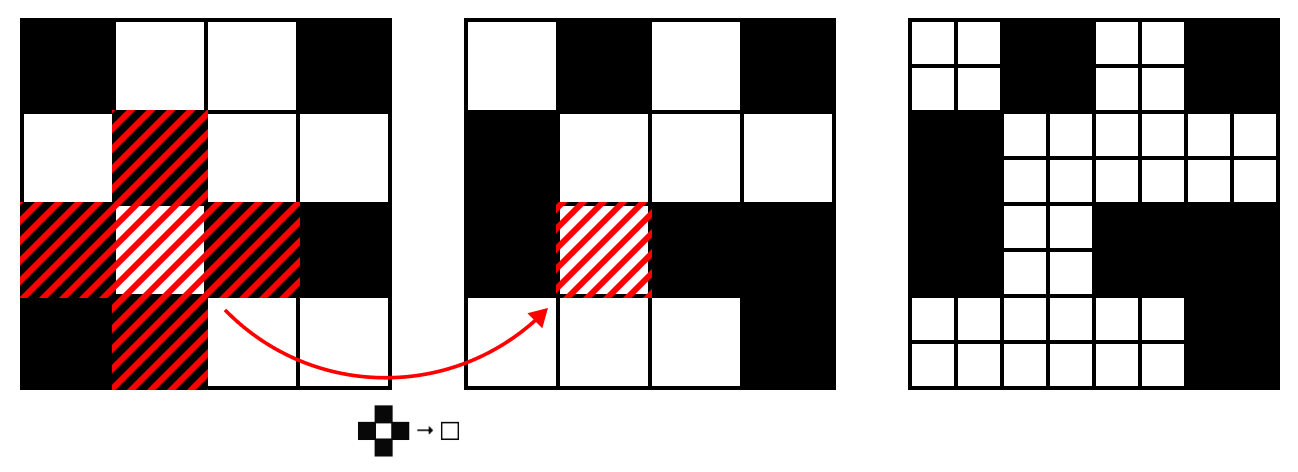In the third picture it's unclear whether black cells divided or not. Trust me, they did. Not going to redo the picture.
Repeat the procedure a few times. You'll get something like this:
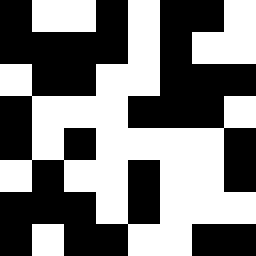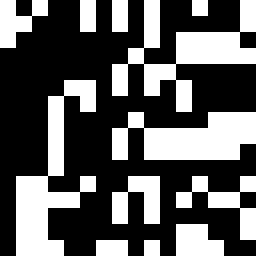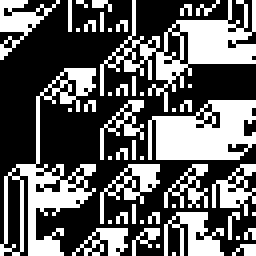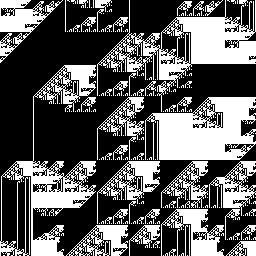
Or this:
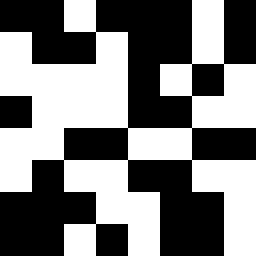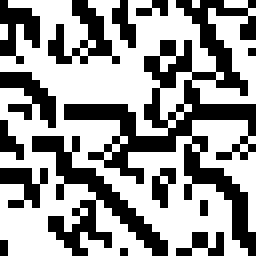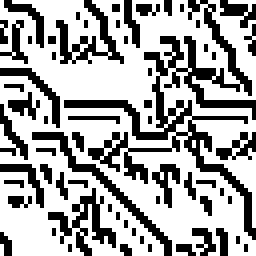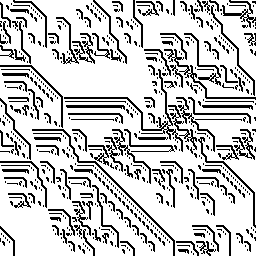
Then you can create coloring rules, combine results from several automata with different rules, switch rules halfway through, overlay the picture on its previous iterations, have full-on fun!
One downside: 3D ivanomata aren't nearly as cool.