In school we studied graphs of various functions, for example, parabolas: y = x². I couldn't understand why when increasing x, like y = (x + 1)², the graph shifts left. Intuition said it should shift right!
Then it got worse: turns out when multiplying x, y = (2x)², the graph doesn't stretch along the x-axis but instead compresses.
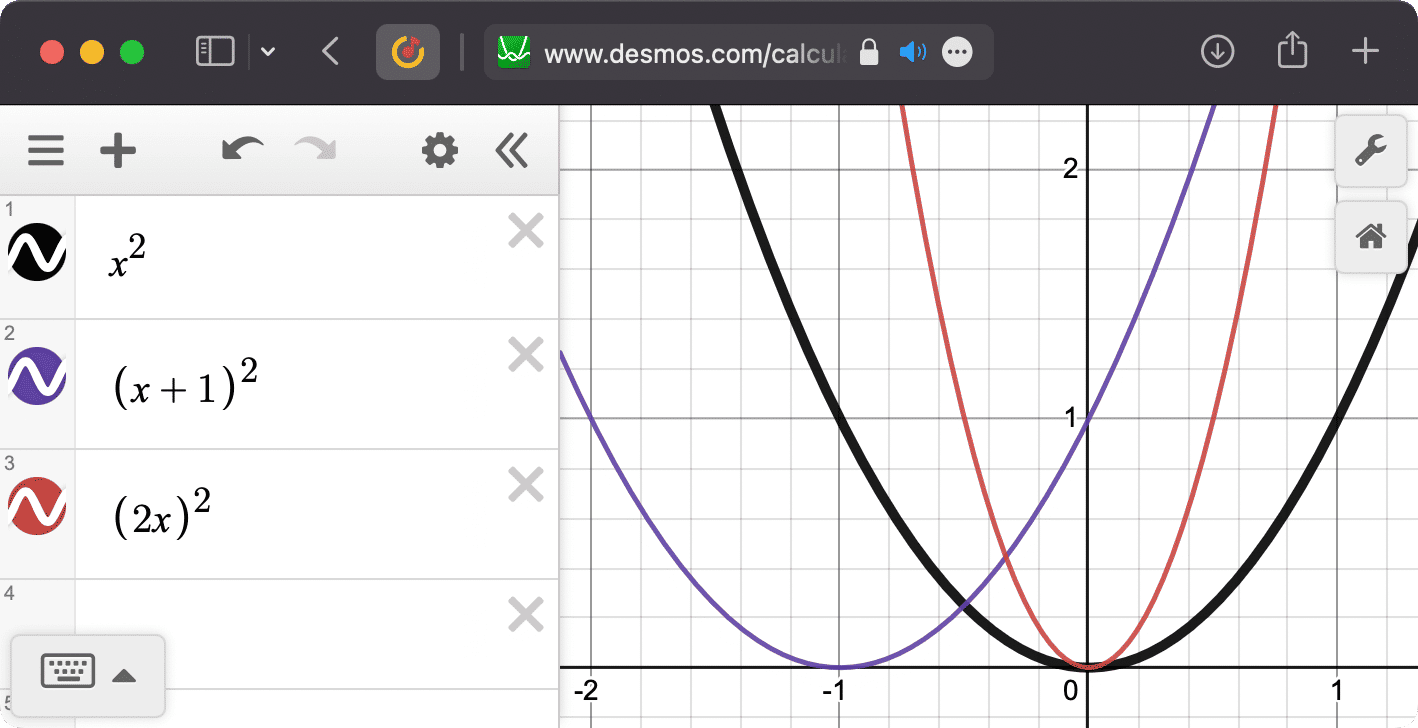
If you don't believe me, check for yourself.
When I started digging into shaders, it turned out school problems still weren't solved. So the first year I picked the right operator by trial and error: plus didn't help, okay, let's try minus.
Now I think I've figured it out, let me explain.
Take a shader that draws a circle:

precision highp float;
uniform vec2 resolution;
out vec4 outColor;
void main(){
vec2 uv=(gl_FragCoord.xy*2.-resolution)/resolution.y*2.; // find UV coordinates of a pixel
outColor.rg+=fract(uv); // draw grid while space is not transformed yet
outColor.b=1.; // nice colors!
// TRANSFORMATIONS WILL BE HERE
outColor+=step(length(uv),1.); // draw circle in transformed space
// it's like pixel is saying "if my distance to the origin is less than 1, I go white"
}
Indeed, uv*=2.; shrinks the image:
and uv/=2.; stretches it:
Similarly uv.x += 1.; shifts the graph left, and uv.x -= 1. — right. Where's the logic, where's reason?
For a while I thought I found salvation in this formulation:
When we transform coordinates, we're not changing the image but the space. For example, if we do
uv*=2.;, all changes in space start happening twice as fast, so the circle shrinks.
But using this idea while programming was difficult. Finally a more convenient thought came:
When we change a point's coordinates, it starts pretending to be another point with new coordinates.
Let's say, a pixel. We calculate its uv coordinates and get (0, 0.5). After multiplying each component by 2, this pixel will pretend to be point (0, 1), which is the right edge of our unit circle. So our pixel will show that edge.
It turns out the circle edge became twice as close to the center than it would be without the transformation.
Exercises: Take the original shader with the circle and add a transformation to make the circle:
- shift down by 1.;
- compress along the y-axis 4 times;
- have radius 0.5 and center at (0.5, 0.5)
What do you think about this way of thinking about space transformations? What remained unclear? Or maybe you know an easier way to explain transformations? Tell me in the comments here or write to my telegram.

