Иваноматы — клеточные автоматы с нарастающим разрешением. Вроде бы, таких раньше не было, поэтому назвал в свою честь. Если вы что-то похожее уже видели, дайте знать, перееименую.
Как-то раз читал на ночь книжку «The Algorithmic Beauty of Plants» и понял, что клеточные автоматы — частный случай контекстно-зависимых L-систем! А ведь я два года пытался и не мог придумать, как сделать генеративные грамматики двумерными.
Так вдохновился, что следующим утром написал прототип.
Как работает
Клеточному автомату нужны правила, по которым клетки меняют цвета.
Цветов у нас всего два: ■ и □. Чтобы найти новый цвет клетки, посмотрим, какого цвета она сама и её четыре соседа. Возможны 32 комбинации:
Каждой из этих комбинаций сопоставим цвет, в который перекрасим центральную клетку, это и будут наши правила. Например, такие:
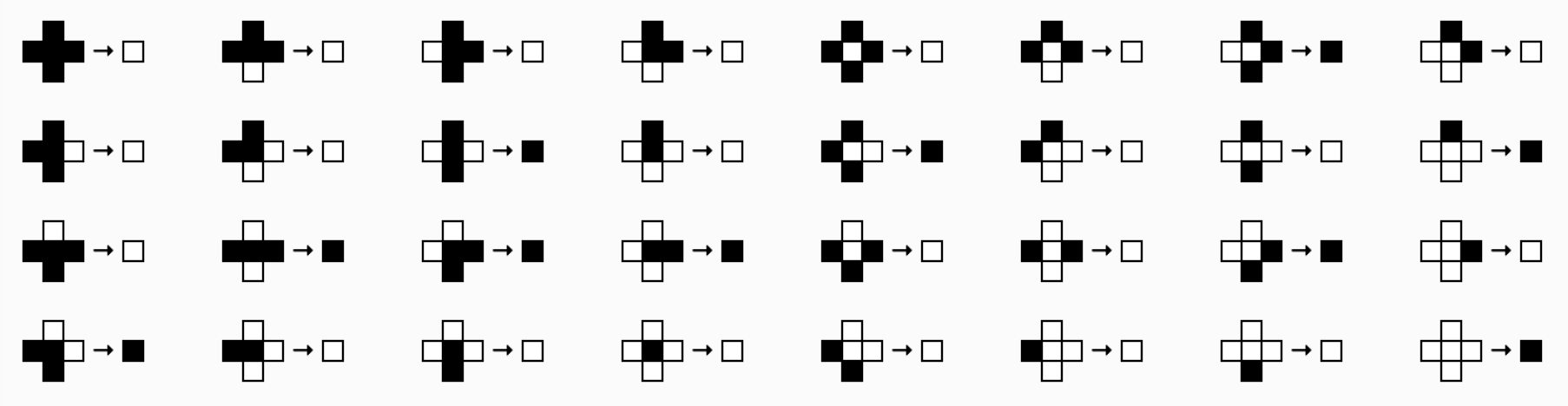Это один из 232 = 4 294 967 296 возможных вариантов правил
Дальше просто. Берём табличку 4×4 клетки, рандомно заполняем □ и ■.
Проходимся по ней правилами, находим новые цвета для каждой ячейки. Обратите внимание, как центральная клетка заштрихованного участка использовала подходящее правило, чтобы узнать свой новый цвет.
И, наконец, увеличиваем разрешение таблицы: каждую клетку делим на четыре.
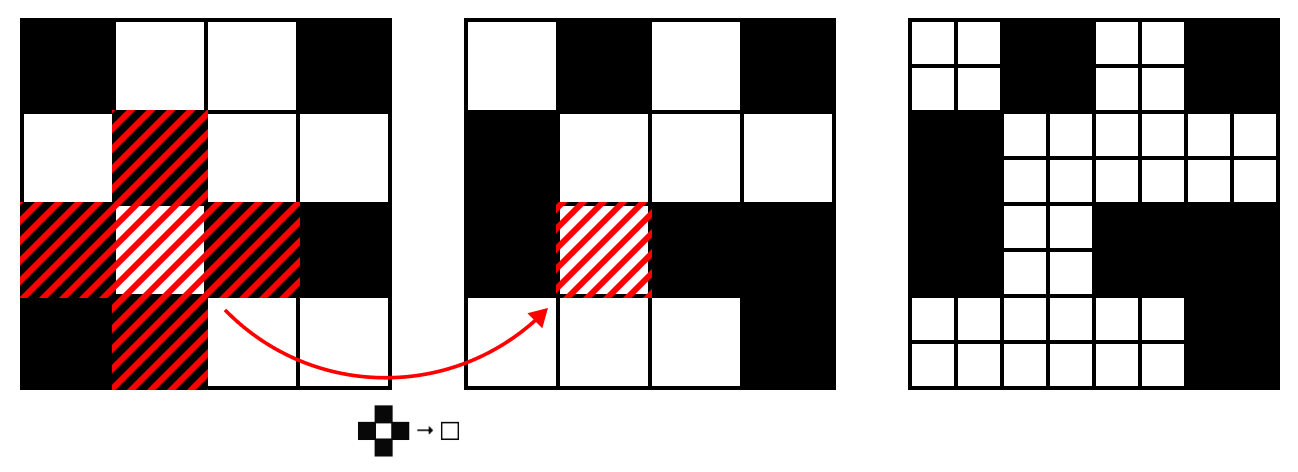На третьей картинке получилось непонятно, разделились чёрные клетки или нет. Поверьте мне, что разделились. Не переделывать же картинку.
Повторяем процедуру несколько раз. Будет получаться что-то такое:
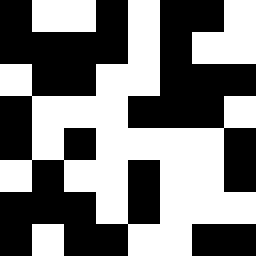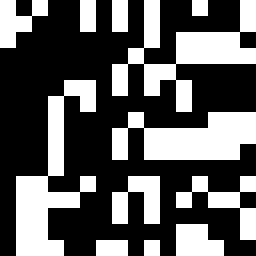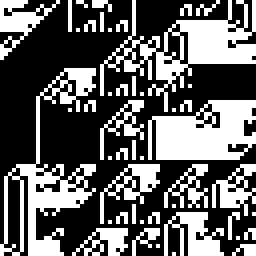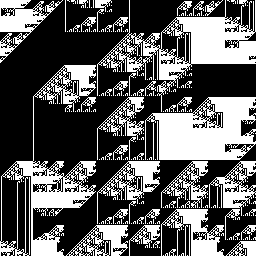
Или такое:
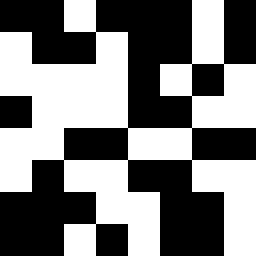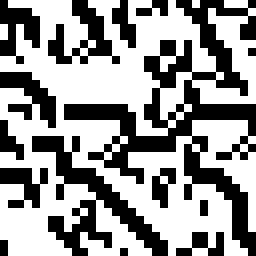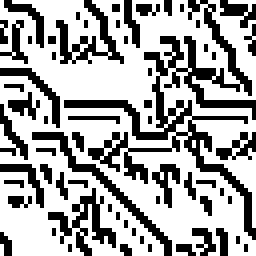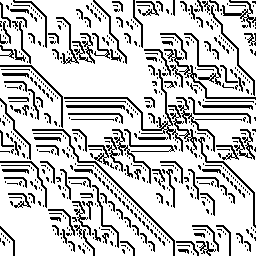
Дальше можно придумать правила раскрашивания, совмещать результаты работы нескольких автоматов с разными правилами, менять правила на полдороге, накладывать картинку на её предыдущие итерации, веселиться по-полной!
Одна печаль, в 3д иваноматы совсем не такие прикольные.