В школе мы проходили графики разных функций, например, параболы: y = x². Я никак не мог понять, почему при увеличении x, например y = (x + 1)² график сдвигается влево. Интуиция говорила, что должен вправо сдвигаться!
Дальше хуже: оказалось, что при умножении икса y = (2x)² график не растягивается вдоль оси x а наоборот, сужается.
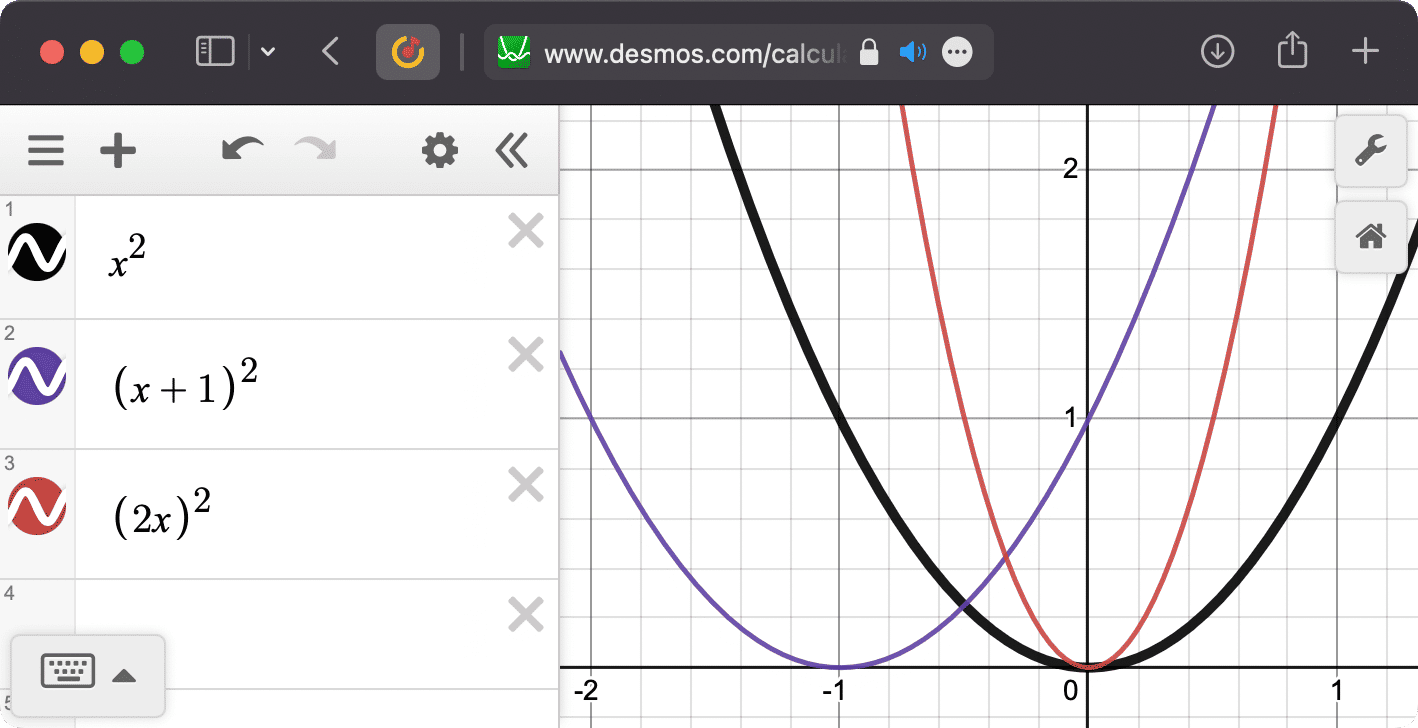
Если не верите, проверьте сами.
Когда начал копать шейдеры, оказалось, что школьные проблемы до сих пор не решены. Поэтому первый год я подбирал нужный оператор методом тыка: плюс не помог, окей, поставим минус.
Сейчас, вроде, разобрался, сейчас расскажу.
Возьмём шейдер, который рисует кружочек:

precision highp float;
uniform vec2 resolution;
out vec4 outColor;
void main(){
vec2 uv=(gl_FragCoord.xy*2.-resolution)/resolution.y*2.; // find UV coordinates of a pixel
outColor.rg+=fract(uv); // draw grid while space is not transformed yet
outColor.b=1.; // nice colors!
// TRANSFORMATIONS WILL BE HERE
outColor+=step(length(uv),1.); // draw circle in transformed space
// it's like pixel is saying “if my distance to the origin is less than 1, I go white”
}
Действительно, uv*=2.; уменьшает картинку:
а uv/=2.; растягивает её:
Аналогично uv.x += 1.;. сдвигает график влево, а uv.x -= 1. — вправо. Где логика, где разум?
На какое-то время я думал, что нашёл спасение в вот такой формулировке:
Когда мы трансформируем координаты, мы меняем не картинку а пространство. Например, если делаем
uv*=2.;, все изменения в пространстве начинают происходить в два раза быстрее, вот кружок и уменьшается.
Но пользоваться такой мыслью при программировании было сложно. Наконец придумалась более удобная:
Когда мы меняем координаты точки, она начинает притворяться другой точкой с новыми координатами.
Допустим, пиксель. Вычисляем его uv координаты и получаем (0, 0.5). После умножения каждого компонента на 2 этот пиксель притворится точкой (0, 1), а это правый край нашей единичной окружности. Значит наш пиксель этот край и покажет.
Получилось, что край окружности стал в два раза ближе к центру, чем был бы без трансформации.
Упражнения: Возьмите исходный шейдер с кружком и добавьте трансформацию, чтобы окружность:
- сдвинулась вниз на 1.;
- скукожилась по оси y в 4 раза;
- стала с радиусом 0.5 и с центром в (0.5, 0.5)
Что думаете про такой способ думать о трансформациях пространства? Что осталось непонятным? А может, вы знаете, как проще трансформации объяснить? Расскажите тут в комментариях или напишите мне в телеграм.

