Концепт ID в шейдерах

Расскажу про концепцию идентификатора в шейдерах и покажу, на что она способна. Если вы не знакомы с шейдерами и вам ничего непонятно, начните с книги шейдеров — лучшего учебника по сабжу.

Примеры кода из статьи можно запустить в клёвом редакторе Твигл, в режиме geekest (es300)

Цель приёма — усложнить картинку и получить контроль над каждым из крошечных участков.

Сперва опишу алгоритм, потом проиллюстрирую приём кодом и картинками. Алгоритм такой:

0. Задаём всем пикселям одинаковый начальный id. Например, пусть будет равен единице.
1. Делим пиксели на группы. То, в какую группу попадёт пиксель, зависит от его id, полученному на предыдущем шаге. Получаем новые идентификаторы.
2. Повторяем пункт 1 несколько раз, каждый раз увеличивая число возможных id и усложняя картинку.
3. Используем id для расчёта цвета, текстуры, скорости анимации, чего угодно.

Есть два способа вычислять id: аккуратный и хаотичный. Затестим оба:

Аккуратный способ сегментации

Допустим, мы хотим каждый раз делить картинку на три части. А ещё допустим, что мы аккуратные и хотим гарантировать, что ни у каких двух сегментов айдишники не совпадут, сколько бы их ни было.

Есть способ добиться желаемого: при первом делении раздадим каждой части айдишники от 0 до 1, чтобы они были «на одинаковом расстоянии» друг от друга: id = 0, id = 1/3, id = 2/3. При следующем делении каждой трети ещё на три части, прибавим к уже найденным айдишникам уменьшенные значения: id = id + 0, id = id + 1/9, id = id + 2/9. Каждое следующее деление должно менять айдишник с меньшим и меньшим шагом.

При таком алгоритме мы можем гарантировать уникальность каждого айдишника, ура. Попробуем повторить идею в коде:

vec2 uv = FC.xy/r;

float id=0., k=1.;

uv=fract(uv)*3.;

id+=floor(uv.x)/3.; // делим на три столбца
k/=3.;
id+=k*floor(uv.y)/3.; // делим на три строки
k/=3.;

uv=fract(uv)*3.;

id+=k*floor(uv.x)/3.; // делим на три столбца
k/=3.;
id+=k*floor(uv.y)/3.;  // делим на три строки
k/=3.;

o+=id;

Мы видим, что каждый сегмент имеет свой уникальный цвет, но для этого приходится использовать мультипликатор k, что не всегда удобно. Часто бывает достаточно хаотического подхода.

Хаотический способ сегментации

В прошлый раз мы аккуратно прибаляли к разным частям сегмента три разных значения.

Здесь мы также используем предыдущее значение айдишника сегмента, чтобы найти айдишкики трёх кусочков. Разница в используемой функции, тут это псевдорандом: функция, которая принимает на вход любое число (seed) и возвращает случайное число от 0 до 1. Прикол в том, что для одного и того же аргумента seed она возвращает одно и то же случайное значение.

↓ id подсегмента             ↓ id сегмента
id = rnd( floor(uv.y) / 3. + id )
         └─────────────────────┘  seed
         └────────────────┘ штука,
         которая делает seed разным
         для разных частей сегмента

Код:

#define rnd(x) fsnoise(vec2(x))
vec2 uv = FC.xy/r;

float id=0.;

uv=fract(uv)*3.;

id=rnd(floor(uv.x)/3.);  // делим на три столбца
id=rnd(floor(uv.y)/3.+id);  // делим на три строки

uv=fract(uv)*3.;

id=rnd(floor(uv.x)/3.+id);  // делим на три столбца
id=rnd(floor(uv.y)/3.+id);  // делим на три строки

o+=id;

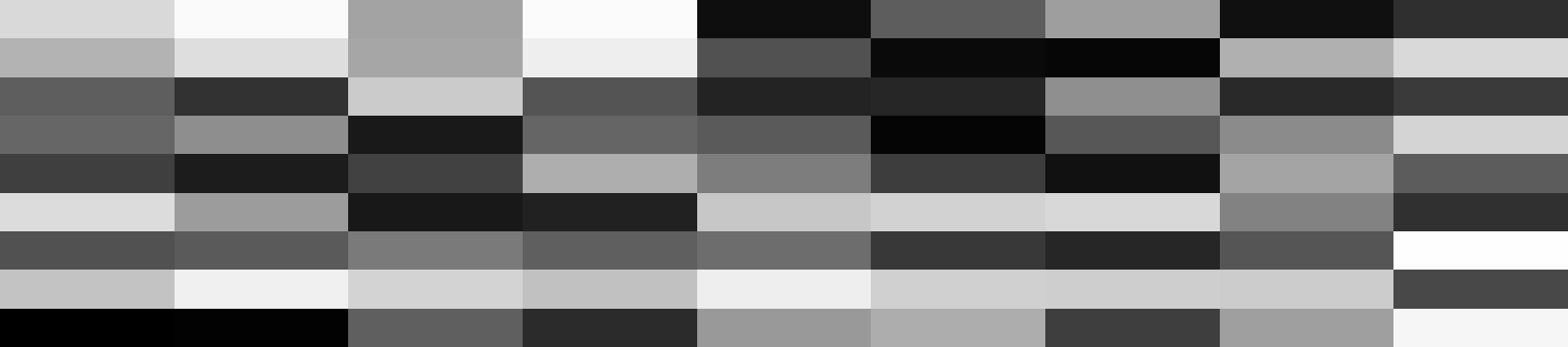
Видим, что сетка получается хаотичной, может у каких-то регионов айдишники и совпадут, но вероятность маленькая.

Изменчивость сегментов

Пристегните ремни. Сейчас самое крутое. Можно сделать настройки последующих разбиений зависимыми от текущего айдишника. Буум!

Например, тут число разбиений может варьировать в зависимости от айди:

#define rnd(x) fsnoise(vec2(x)+.1)
vec2 uv = FC.xy/r;

float id=0.;

uv=fract(uv)*3.;

id=rnd(floor(uv.x)/3.);  // делим на три столбца
id=rnd(floor(uv.y)/3.+id);  // делим на три строки

uv=fract(uv)*3.;

//                 ↓ чем меньше, тем гуще
id=rnd(floor(uv.x/id)/3.+id);  // делим на три столбца
id=rnd(floor(uv.y/id)/3.+id);  // делим на три строки

o+=id;

Можно повторять и повторять разбиение сколько угодно. Или лучше добавить цикл, чтобы не копипастить.

#define rnd(x) fsnoise(vec2(x)+.1)
vec2 uv = FC.xy/r;

float id=1.;

for(int i=0;i<3;i++){
  uv=fract(uv)*3.;
  id=rnd(floor(uv.x/id)/3.+id);
  id=rnd(floor(uv.y/id)/3.+id);
}

o+=id;

Если увеличить число повторов до 5, останется один мусор:

Но ведь мы можем сделать число повторов цикла также зависимым от id!

#define rnd(x) fsnoise(vec2(x)+.1)
vec2 uv = FC.xy/r;

float id=1.;

for(int i=0;i<5;i++){
  uv=fract(uv)*3.;
  id=rnd(floor(uv.x/id)/3.+id);
  id=rnd(floor(uv.y/id)/3.+id);
  if(i>0 && id<.5) break;
}

o+=id;

Картинка потемнела, это что-то вроде ошибки выжившего. Мы вылетаем из цикла, когда айдишник меньше .5, а у таких цвет получается тёмным. Это исправляется заменой условия id < .5 на rnd(id) < .5

А теперь, когда приём освоен, можно идти и веселиться по-полной.

#define rnd(x) fsnoise(vec2(x)+.1)
#define rot(a) mat2(cos(a),-sin(a),sin(a),cos(a))

vec2 uv = (FC.xy*2.-r)/r.x;

float id=floor(length(uv)*8.)+1.;

for(int i=0;i<5;i++){
  if(i>0 && rnd(id)<.5) break;
  uv*=rot(PI/4.+t*(rnd(id)-.5));
  uv=fract(uv)*3.;
  id=rnd(floor(uv.x/id)/3.+id);
  id=rnd(floor(uv.y/id)/3.+id);
}

o+=id;

Посмотрите ссылку, оно ещё и крутится! Скорость вращения каждого кусочка, конечно же, зависит от его айдишника.